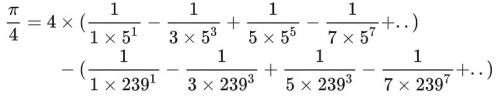Π:修订间差异
跳到导航
跳到搜索
(创建页面,内容为“π 的定义: π(圆周率)是圆的周长与直径的比值,等于圆形之面积与半径平方之比,sinx=0的最小正数 === π 的简史 === # 四千年前,巴比伦人用 3+ 1/8 作为圆周率, 同时期的埃及人用 4-(8/9)^2 作为圆周率 # 公元前三世纪,古希腊科学家阿基米德首先采用计算的方法,得出 π 可能是 3.14 # 中国古算书《周髀算经》(约公元前 2 世纪)的中有“径一而周三…”) |
无编辑摘要 |
||
| (未显示同一用户的4个中间版本) | |||
| 第1行: | 第1行: | ||
π 的定义: | π 的定义: | ||
π(圆周率)是圆的周长与直径的比值,等于圆形之面积与半径平方之比,sinx= | π(圆周率)是圆的周长与直径的比值,等于圆形之面积与半径平方之比,sinx=0 的最小正数 | ||
=== π 的简史 === | === π 的简史 === | ||
# 四千年前,巴比伦人用 3+ 1/8 作为圆周率, 同时期的埃及人用 4-(8/9)^2 作为圆周率 | # 四千年前,巴比伦人用 3+ 1/8 作为圆周率, 同时期的埃及人用 4-(8/9)^2 作为圆周率 | ||
# 公元前三世纪,古希腊科学家阿基米德首先采用计算的方法,得出 π | # 公元前三世纪,古希腊科学家阿基米德首先采用计算的方法,得出 π 可能是 3.14 | ||
# 中国古算书《周髀算经》(约公元前 2 世纪)的中有“径一而周三”的记载,用 3 作为圆周率 | # 中国古算书《周髀算经》(约公元前 2 世纪)的中有“径一而周三”的记载,用 3 作为圆周率 | ||
# 公元五世纪,中国数学家祖冲之把 π 算到了 3.1415926 到 3.1415927 之间 | # 公元五世纪,中国数学家祖冲之把 π 算到了 3.1415926 到 3.1415927 之间 | ||
# 公元 15 世纪,阿拉伯数学家阿尔·卡西 (Al-Kāshī,1380?– 1429),用几何的方法,计算到了小数点后 16 位 | # 公元 15 世纪,阿拉伯数学家阿尔·卡西 (Al-Kāshī,1380?– 1429),用几何的方法,计算到了小数点后 16 位 | ||
# 1666 年, 牛顿计算到了小数点后的 15 位,但这个公式的收敛速度较慢 | # 1666 年, 牛顿计算到了小数点后的 15 位,但这个公式的收敛速度较慢 | ||
# | # 1706 年,英国数学家和天文学家约翰·梅钦(John Machin) 发明了一个用于计算 π 值的公式,收敛速度非常快 | ||
# 1873 年, William Shanks 使用梅钦公式用了几年时间,计算到了小数点后的 707 位,还刻到了其墓碑上。但 50 多年后(20 世纪 30 年代),被新西兰数学家发现第 528 位有一个计算错误 | # 1873 年, William Shanks 使用梅钦公式用了几年时间,计算到了小数点后的 707 位,还刻到了其墓碑上。但 50 多年后(20 世纪 30 年代),被新西兰数学家发现第 528 位有一个计算错误 | ||
# | # 1949 年,ENIAC(Electronic Numerical Integrator And Computer, 电子数字积分计算机)计算机用了 70 个小时,计算到了小数点后的 2037 位 | ||
# | # 2021 年 8 月 17 日,瑞士研究人员使用一台超级计算机,历时 108 天,计算到小数点后 62.8 万亿位 | ||
# 2021 年 10 月 14 日,谷歌使用 128 个 VCPU 和 864 GB RAM,515 TB 存储,历时近 158 天,计算到小数点后 100 万亿位 | |||
# 2023 年 3 月 1 日,阿奔使用 3 个 Ampere A1 VCPU 和 18 GB RAM,57 GB 存储,历时近 1 秒,计算到小数点后 1 万位,后四位数字:5678 | |||
=== 计算公式 === | === 计算公式 === | ||
计算 π 值的主要公式有: | 计算 π 值的主要公式有: | ||
* 梅钦(John Machin)公式(1706) | * 梅钦(John Machin)公式(1706) | ||
* 拉马努金( Srinivasa Ramanujan )公式(1914) | * 拉马努金(Srinivasa Ramanujan)公式(1914) | ||
* BBP (David Bailey / Peter Borwein / Simon Plouffe)公式(1996) | * BBP (David Bailey / Peter Borwein / Simon Plouffe)公式(1996) | ||
==== 梅钦(John Machin)公式 ==== | ==== 梅钦(John Machin)公式 ==== | ||
π = | π = 16 × arctan(1/5) - 4 × arctan(1/239) | ||
其 Taylor 级数展开式为: | 其 Taylor 级数展开式为: | ||
[[文件:Machin-pi.jpg|无框|500x500像素]] | [[文件:Machin-pi.jpg|无框|500x500像素]] | ||
==== 梅钦公式的 Python 实现 ==== | |||
<small>n = 100 | |||
t = n+10 | |||
b = 10**t | |||
x1 = b*4//5 | |||
x2 = b // -239 | |||
s = x1+x2 | |||
n *= 2 | |||
for i in range(3, n, 2): | |||
x1 //= -25 | |||
x2 //= -57121 | |||
x = (x1+x2) // i | |||
s += x | |||
pai = s*4 | |||
pai //= 10**10 | |||
print(pai)</small> | |||
结果: | |||
3.1415 9265 3589 7932 3846 2643 3832 7950 2884 1971 6939 9375 1058 2097 4944 5923 0781 6406 2862 0899 8628 0348 2534 2117 0679 [[分类:Doc]] | |||
[[分类:Help]] | |||
2024年3月28日 (四) 17:11的最新版本
π 的定义:
π(圆周率)是圆的周长与直径的比值,等于圆形之面积与半径平方之比,sinx=0 的最小正数
π 的简史
- 四千年前,巴比伦人用 3+ 1/8 作为圆周率, 同时期的埃及人用 4-(8/9)^2 作为圆周率
- 公元前三世纪,古希腊科学家阿基米德首先采用计算的方法,得出 π 可能是 3.14
- 中国古算书《周髀算经》(约公元前 2 世纪)的中有“径一而周三”的记载,用 3 作为圆周率
- 公元五世纪,中国数学家祖冲之把 π 算到了 3.1415926 到 3.1415927 之间
- 公元 15 世纪,阿拉伯数学家阿尔·卡西 (Al-Kāshī,1380?– 1429),用几何的方法,计算到了小数点后 16 位
- 1666 年, 牛顿计算到了小数点后的 15 位,但这个公式的收敛速度较慢
- 1706 年,英国数学家和天文学家约翰·梅钦(John Machin) 发明了一个用于计算 π 值的公式,收敛速度非常快
- 1873 年, William Shanks 使用梅钦公式用了几年时间,计算到了小数点后的 707 位,还刻到了其墓碑上。但 50 多年后(20 世纪 30 年代),被新西兰数学家发现第 528 位有一个计算错误
- 1949 年,ENIAC(Electronic Numerical Integrator And Computer, 电子数字积分计算机)计算机用了 70 个小时,计算到了小数点后的 2037 位
- 2021 年 8 月 17 日,瑞士研究人员使用一台超级计算机,历时 108 天,计算到小数点后 62.8 万亿位
- 2021 年 10 月 14 日,谷歌使用 128 个 VCPU 和 864 GB RAM,515 TB 存储,历时近 158 天,计算到小数点后 100 万亿位
- 2023 年 3 月 1 日,阿奔使用 3 个 Ampere A1 VCPU 和 18 GB RAM,57 GB 存储,历时近 1 秒,计算到小数点后 1 万位,后四位数字:5678
计算公式
计算 π 值的主要公式有:
- 梅钦(John Machin)公式(1706)
- 拉马努金(Srinivasa Ramanujan)公式(1914)
- BBP (David Bailey / Peter Borwein / Simon Plouffe)公式(1996)
梅钦(John Machin)公式
π = 16 × arctan(1/5) - 4 × arctan(1/239)
其 Taylor 级数展开式为:
梅钦公式的 Python 实现
n = 100
t = n+10
b = 10**t
x1 = b*4//5
x2 = b // -239
s = x1+x2
n *= 2
for i in range(3, n, 2):
x1 //= -25
x2 //= -57121
x = (x1+x2) // i
s += x
pai = s*4
pai //= 10**10
print(pai)
结果:
3.1415 9265 3589 7932 3846 2643 3832 7950 2884 1971 6939 9375 1058 2097 4944 5923 0781 6406 2862 0899 8628 0348 2534 2117 0679