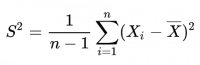随机变量
随机变量(random variable)表示随机试验各种结果的实值单值函数。
随机事件不论与数量是否直接有关,都可以数量化,即都能用数量化的方式表达。
随机事件数量化的好处是可以用数学分析的方法来研究随机现象。
例如某一时间内公共汽车站等车乘客人数,电话交换台在一定时间内收到的呼叫次数,灯泡的寿命等等,都是随机变量的实例。
基本类型
按照随机变量可能取得的值,可以把它们分为两种基本类型:
- 离散型
离散型(discrete)随机变量即在一定区间内变量取值为有限个或可数个。
离散型随机变量通常依据概率质量函数分类,主要分为:伯努利随机变量、二项随机变量、几何随机变量和泊松随机变量。
例如某地区某年人口的出生数、死亡数,某药治疗某病病人的有效数、无效数等。
- 连续型
连续型(continuous)随机变量即在一定区间内变量取值有无限个,或数值无法一一列举出来。
有几个重要的连续随机变量常常出现在概率论中,如:均匀随机变量、指数随机变量、伽马随机变量和正态随机变量。
例如某地区男性健康成人的身长值、体重值,一批传染性肝炎患者的血清转氨酶测定值等。
数学期望(mathematic expectation)
- 离散型
如果 X 是离散随机变量,数学期望是可能取的值的加权平均。简单来说就是所有值的算术平均。
- 连续型
如果 X 是具有概率密度函数 f(x) 的连续随机变量,那么在上均匀分布的随机变量的期望值正是区间的中点。
记为:E(X)
方差(variance/deviation Var)
在统计描述中,方差用来计算每一个变量(观察值)与总体均数之间的差异。统计学采用平均离均差平方和来描述变量的变异程度。
S2 为样本方差,X 为变量,x̅ 为样本均值,n 为样本例数
记为:D(X), DX, Var(X)
方差的计算公式有个令人迷惑的地方:
总体时分母是 N,样本时分母是 n-1。
实际上,求总体方差时,每个出现的概率为 N 分之一,因为每一项都是自由变换的。而样本是除以 (n-1) 实际上也是乘的概率,样本的 n 项其实如果确定了 (n-1) 项第 n 项就百分百确定,所以每一项出现的概率只有 (n-1) 分之一。方差说的是概率,不是有多少个。
标准差(Standard Deviation)
也称为均方差,为方差的算术平方根。标准差是用来衡量一组数据的离散程度的统计量。
协方差(Covariance)
协方差是一个反映两个随机变量相关程度的指标。从直观上来看,协方差表示的是两个变量总体误差的期望。
Cov(X,Y) = E[(X-E[x])(Y-E[Y])]
比如,要研究3种肥料对苹果产量的实际效应,而各棵苹果树头年的“基础产量”不一致,但对试验结果又有一定的影响。要消除这一因素带来的影响,就需将各棵苹果树第1年年产量这一因素作为协变量进行协方差分析,才能得到正确的实验结果。
协方差能反映两个随机变量的相关程度(协方差大于0的时候表示两者正相关,小于0的时候表示两者负相关),但是协方差值的大小并不能很好地度量两个随机变量的关联程度,例如,现在二维空间中分布着一些数据,我们想知道数据点坐标X轴和Y轴的相关程度,如果X与Y的相关程度较小但是数据分布的比较离散,这样会导致求出的协方差值较大,用这个值来度量相关程度是不合理的。
皮尔逊相关系数(Pearson Correlation Coefficient)
Pearson 相关系数是用协方差除以两个变量的标准差得到的。
pearson 是一个介于 -1 和 1 之间的值,当两个变量的线性关系增强时,相关系数趋于 1 或 -1。
其实主要问题在于 cov(kx, y)=k cov(x,y),量纲对协方差的影响很大,因此,才要将x,y标准化,皮尔逊相关系数其实就是标准化后的协方差。 适用条件:
- 两个变量分别服从正态分布;(当数据量够大时,譬如 n>30 ,根据中心极限定理,可以假定服从正态分布)
- 两个变量的标准差不为0(通常都满足);
显著性检验:
通常使用 t 检验来验证 Pearson 相关系数的显著性
t 检验
亦称 student t 检验(Student's t test),主要用于样本含量较小(例如n<30),总体标准差 σ 未知的正态分布。t 检验是用 t 分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著。它与 f 检验、卡方检验并列。